@AFC_cristal
Distance entre plans réticulaires dans un réseau hexagonal
Tout d'abord, souvenez vous des caractèristiques du réseau réciproque hexagonal:
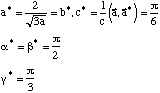
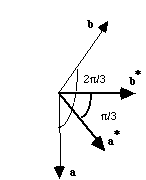
Donc
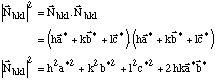
Les autres termes sont nuls car : cos α* = cos β* = 0
donc:
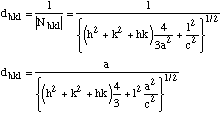
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Rangée commune à deux plans réticulaires (fin)
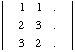
u = 2x2 - 3x3 = -5
v = 3x1 - 1x2 = 1
w = -1x2 + 3x1 = 1
Donc, R, la rangée recherchée, a pour indices [-511] ou [5-1-1], ce qui revient au même.
Attention ! Si les trois nombres obtenus n'avaient pas été premiers entre eux, il aurait fallu les diviser par leur plus grand commun diviseur.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Indices de Miller - suite
Vraiment la cristallographie ne vous inspire pas ! Vous tenez vraiment trop à votre origine. Il me semble que vous devriez reprendre à sa base.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Plan du cours
Vous pouvez parcourir ce cours depuis le début, ce que je vous conseille, ou accéder directement aux notions essentielles. Je pense que ce deuxième usage devrait être réservé à des révisions uniquement, jamais à un premier usage.
- Introduction
- Début
- Produit scalaire
- Produit vectoriel
- Réseau réciproque
- Notions sur les rangées réticulaires
- Notions sur les plans réticulaires
- Angle entre plans
- Rangée commune à deux plans
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Indices de Miller
Soient : OA = x.a
OB = y.b
OC = z.c
où x, y, z sont des entiers
Prenons leurs inverses 1/x, 1/y, 1/z et multiplions les par leur plus petit commun multiple.
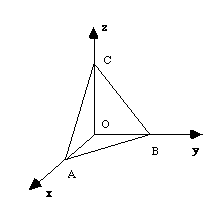
On obtient trois nombres premiers entre eux h,k,l qui sont les indices de Miller du plan considéré.
Les indices de Miller d'un plan sont notés entre des parenthèses : (h,k,l).
Si vous n'aimez pas les mathématiques, sautez les quelques lignes suivantes et passez directement à la question qui est posée.
L'équation du plan ABC s'écrit
h x + k y + l z = N
Vous pouvez le vérifier aux points A, B, C ; la constante N est nulle lorsque le plan passe par l'origine.
Question : Si le repère est construit sur une maille multiple, les nombres x, y, z sont-ils toujours entiers ?
- Oui.
- Non.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Recommencez!
Hum! Êtes-vous vraiment en train d'étudier les bases de la cristallographie géométrique ? Revenez au départ et réfléchissez bien !!!
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Produit scalaire - suite
Vous vous souvenez certainement de la définition suivante du produit scalaire de deux vecteurs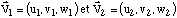 
:
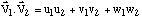
Cette écriture sous-entend que le repère sur lequel les vecteurs sont exprimés est orthonormé ! Cela signifie :
- que le repère est orthogonal.
Si on développe le produit scalaire sur la base a, b, c il se simplifie puisque
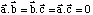
Le produit scalaire se réduit donc à
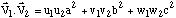
- que le repère est normé.
Si le repère est normé les longueurs des vecteurs de la base sont toutes égales et prises comme unité, donc
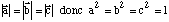
et
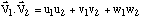
Vous avez maintenant compris votre erreur ?
- Oui ?
- Non ?
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Produit vectoriel - résultat du calcul
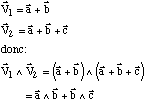
Si la base est quelconque, il n'est pas évident d'exprimer le vecteur résultant sur la base a, b, c. et le produit vectoriel devient donc très difficile à calculer.
De plus, en cristallographie, nous ne nous intéressons qu'aux vecteurs qui pointent sur les noeuds du réseau, c'est à dire à ceux dont les composantes sont entières lorsqu'on les exprime dans une maille primitive.
A priori, le résultat du calcul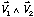 
n'a aucune chance de donner un vecteur de coordonnées entières donc le résultat n'exprime pas un vecteur de l'espace cristallographique.
Si nous revenons au résultat trouvé pour ce même exercice lorsque la base est orthogonale, nous avions trouvé :
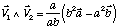
Ce vecteur, bien que nous connaissions son expression sur la base a, b, c, n'appartient pas non plus à l'espace cristallographique, car ses composantes ne sont pas entières. Le produit vectoriel ne semble donc offrir aucun intérêt pour le cristallographe car il ne sait pas l'exprimer dans la plupart des cas.
Mais, comme nous ne manquont pas de ressources, nous avons trouvé une solution!
Accrochez-vous à votre souris: nous allons introduire le réseau réciproque.
Si vous n'avez pas compris pourquoi j'insiste sur l'idée que les composantes d'un vecteur exprimées sur une base primitive, sont entières, revenons en arrière.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Quelques rappels
Tout d'abord, vérifions que vous avez bien assimilé les définitions du réseau réciproque.
Construisez le réseau réciproque associé au réseau hexagonal.
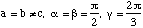
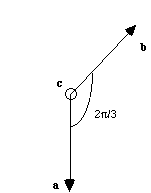
Souvenez-vous des relations scalaires et vectorielles, qui lient les deux réseaux direct et réciproque.
Le cas échéant, si la mémoire vous fait défaut, revenez sur vos pas.
Le plan a*, b* est-il confondu avec le plan a,b?
- Oui ?
- Non ?
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Angle entre plans réticulaires dans un réseau hexagonal
Dans un réseau hexagonal les vecteurs réciproques s'expriment de la façon suivante :
a* et c* sont contenus dans le plan (001).
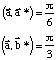
c* est colinéaire à c.
Si vous ne comprenez pas ceci , revoyez l'explication complète.
Calculons la norme de chacune des normales N et N'.
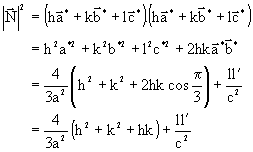
La norme de N' s'obtient en ajoutant le symbole ' derrière chaque indice.
Calculons leur produit scalaire :
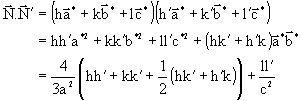
Donc :
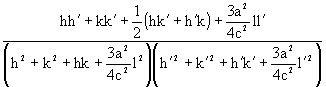
Supposons que a/c = 0,65.
Calculez l'angle entre les plans (101) et (111).
- Il est supérieur à 90 degrés.
- Il est inférieur à à 90degrés.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996