Indices d'une rangée commune à deux plans

Comme nous envisageons l'intersection de deux familles de plans, nous n'allons en réalité déterminer que les indices d'une famille de droites, c'est à dire d'une rangée.

Il existe deux méthodes.

1) - Exprimons les conditions pour qu'une rangée du réseau direct appartienne au plan P.

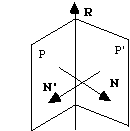
La normale au plan, N, a pour équation :

N = ha* + kb* + lc*

L'expression de la rangée R recherchée est :

R = ua + vb + wc

où u, v, w sont actuellement inconnus et vont être déterminés.

Cette rangée appartient au plan P donc elle est perpendiculaire au vecteur N.

En exprimant cette propriété au moyen d'un produit scalaire, il vient:

R.N = (ua + vb + wc).(ha* + kb* + lc*)

soit: h u + k v + lw = 0

Ce résultat se retrouve en utilisant les relations scalaires qui déterminent le réseau réciproque.

La condition pour que la rangée R appartienne au plan P s'exprime donc par :

h u + k v + lw = 0

De la même façon, on peut exprimer que R est dans le plan P' :

h' u + k' v + l'w = 0

Cette rangée est l'intersection des deux plans: il faut donc résoudre simultanément les deux équations.

Calculez les indices de cette rangée en fonction des indices de Miller des deux plans.

Estimez vous qu'il vous manque une équation?

Par contre si vous pensez avoir le résultat, continuez.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Rangées - suite

Les indices d'une rangée OD sont ceux du vecteur OD soit [111].

Les indices de la rangée OF sont les composantes d'un vecteur colinéaire à OF, OD par exemple ; ce sont donc les mêmes. La convention admise en cristallographie est de choisir comme indices des nombres premiers entre eux.

Considérez à nouveau un réseau quelconque. Plaçez les points de coordonnées A 100, B 010, C 001, D 111, E 222 puis F -1 0 -1.

Calculez les indices de la rangée BF.

Est-ce la même rangée que OD ?

Est-ce une rangée différente ?

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Désolé!

Je crois qu'il est nécessaire que vous appeniez un peu de mathématiques avant de continuer l'étude de la cristallographie.

Ceci m'attriste mais j'ai peur que nous ne puissions rien pour vous !

Actuellement tout au moins ...

Pour vous consoler, dites-vous bien que l'on peut admirer les cristaux sans connaître la cristallographie.

Si vous regrettez le geste qui vous a amené ici, il vous reste la possibilité de revenir en arrière avec la touche "back" de votre butineur.

A bientôt donc!

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Toujours le réseau réciproque

Reprenons les définitions :

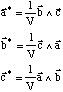
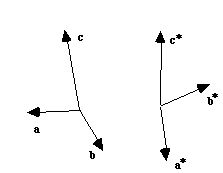
Ces trois relations sont strictement équivalentes aux neuf relations scalaires :

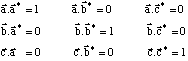
Or, ces dernières sont tout à fait symétriques, c'est-à-dire que a, b, c y jouent un rôle strictement équivalent à a*, b*, c* ; le produit d'un vecteur direct et d'un vecteur réciproque est un nombre sans dimension et si a, b, c s'expriment en Å^-1, V et V*, les volumes des mailles s'expriment donc en ųet Å^-3, respectivement.

Vous vous êtes donc trompé.

Continuez

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Félicitations!

Faites-moi part de vos remarques. Je vous propose de participer à la rédaction de la suite de ce cours qui ne peut absolument pas manquer d'être écrite un jour. Votre collaboration ne peut qu'accélérer cette grande oeuvre bénéfique pour l'humanité entière.

Ou bien vous feuilletez au hasard et, à tout hasard, je vous renvoie en arrière.

Je n'oserais penser que vous ayez l'intention d'utiliser ce cours à un tout autre usage que celui auquel il était primitivement destiné. Il y a des choses qu'on n'ose pas imaginer.

Cristallographie for ever !

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Mais non!

Il paraît a priori gênant de ne disposer que de deux équations pour déterminer trois inconnues u, v et w.

Rappelez-vous qu'on définit les indices d'une rangée à un multiplicateur près : les trois nombres u, v, w ne sont donc pas indépendants. Donc, si on exprime deux inconnues, u et v, en fonction de w, par exemple, on obtiendra un ensemble de trois nombres qu'on réduira ensuite à leur PGCD.

Continuez !

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Indices de Miller

Bravo ! Vous faites des progrès.

Envisageons maintenant le réseau orthogonal dessiné ci-contre.

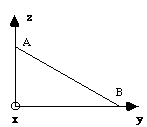
Ce plan posséde-t-il un indice de Miller infini ?

- Oui ?

- Non ?

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Réveillez vous!

Vous êtes vraiment inattentif ! Nous avons déjà expliqué que les indices de Miller étaient inversement proportionnels aux coordonnées des points où le plan coupe les axes. Souvenez-vous de la définition des indices de Miller :

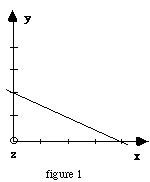
Les indices de Miller du plan (120) correspondent à :

- la figure 1.

- la figure 2.

- Ni l'un ni l'autre, ce plan qui n'est pas dessiné !

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Le réseau réciproque

Soient a, b, c  les trois vecteurs qui définissent une base absolument quelconque.

Nous allons définir la base d'un nouvel espace vectoriel, en introduisant les relations suivantes entre les vecteurs de la base a, b, c et ceux de la nouvelle a*, b*, c*.

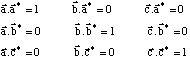
Le réseau construit sur la base a*, b*, c* s'appelle le réseau réciproque.

Lorsqu'on examine ces relations scalaires , celle qui définit a* par exemple, on constate que ce vecteur est perpendiculaire à b et à c.

Remarquez que les unités de mesure sont inverses dans les deux repères: si on exprime les longueurs en angströms, par exemple, dans le réseau direct, l'unité de mesure sera l'inverse, c'est à dire des angströms^-1, dans le réseau réciproque.

Cette dualité des deux réseaux n'est pas évidente à appréhender et nous la découvrirons progressivement dans la suite de ce cours.

On peut montrer que :

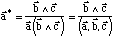
où (a, b, c) est le produit mixte de ces trois vecteurs, c'est-à-dire le volume de la maille directe.

Calculez vous même les expressions de b* et c*.

Vous devez trouver des expressions de la forme de celle que nous venons d'écrire pour a*. Pour effectuer ce calcul utilisez les produits scalaires définis ci-dessus aussi bien pour déterminer l'orientation des vecteurs que leur norme.

Ensuite trouvez les expressions de a, b, c en fonction des vecteurs de base du réseau réciproque.

Le calcul va vous prendre quelque temps.

...... Bonne chance !

Vous avez résolu le problème que je viens de vous poser ?

Quelle que soit votre réponse, cliquez ici.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

NOOOON !

Réfléchissez !

Définir une droite par les composantes d'un vecteur est insuffisant. Il faudrait de plus définir l'origine du vecteur pour l'identifier complètement. En réalité les indices d'une rangée définissent une famille de droites, toutes parallèles entre elles.

Les rangées [242] et [121] sont-elles :

- identiques ?

- différentes ?

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996