@AFC_cristal
C'est la fin!
Vous voici à la fin de ce cours.
J'espère que vous avez compris les éléments essentiels du calcul en cristallographie. Cependant d'autres exercices seront nécessaires pour parfaire vos connaissances.
Vos remarques seront les bienvenues pour améliorer et enrichir ce cours.
Vous seriez gentil de les adresser à l'AFC ici.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Indices de Miller (encore)...
Il semble que vous ayez compris la défintion des indices de Miller d'un plan. Avant que nous n'envisagions de nouvelles connaissances, voulez-vous résoudre l'exercice suivant?
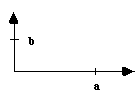
Dans un repère orthogonal tel que le rapport des paramètres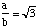 
, trouvez l'angle qui existe entre la rangée [1 -1 0] et la normale au plan (1 -1 0).
Cliquez ici lorsque vous aurez résolu ce problème.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Introduction
Ce cours suppose acquises quelques bases de cristallographie ; il a été conçu pour des étudiants qui auraient lu auparavant le cours programmé de Schenk, par exemple, afin d'être déjà familiarisés avec le vocabulaire.
Et maintenant, tournez la page !
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Normale à un plan
Nous allons maintenant envisager des utilisations du réseau réciproque.
Nous avons vu qu'une rangée d'indices [h,k,l] n'est pas, en général, perpendiculaire au plan d'indices de Miller (h,k,l).
Maintenant exprimons l'équation d'une rangée du réseau réciproque :
N = ha* + kb* + lc*
et imaginons que le réseau direct et le réseau réciproque soient tracés à partir de la même origine. Tracons une rangée R de ce réseau.
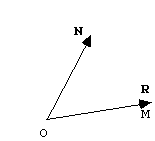
Si tracer les deux réseaux à partir de la même origine vous trouble, retournez en arrière. Pour revenir directement ici, utilisez la touche back de votre fureteur.
Eventuellement, revoyez aussi le dessin des réseaux direct et réciproque hexagonaux.
Soit M un noeud du réseau direct: il est l'extrémité du vecteur OM d'équation:
R = ua + vb + wc
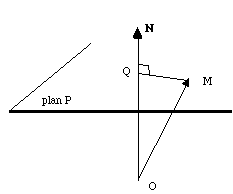
Imaginons que M pointe successivement surtous les noeuds d'un plan P perpendiculaire à N. Ce plan est défini dans le réseau direct puisque OM est un vecteur de ce réseau. La projection de tous les vecteurs OM sur la normale au plan P tracée à partir de O, qui est N, est constante et égale à OQ.
On peut donc écrire : OM.N = OQ.N.
Soit :
OM.ON = (ua + vb + wc).(ha* + kb* + lc*)
OM.ON = hu + kv + lw
Si ce résultat vous étonne, revoyez la définition du réseau réciproque.
Supposons que le réseau soit primitif ; alors h,k,l, d'une part, u,v,w d'autre part, sont entiers et:
hu + kv + lw = K
où K est entier.
Ceci est l'équation du plan d'indices de Miller (h,k,l).
Donc, la normale au plan d'indices de Miller (h,k,l) est la rangée réciproque de composantes [h,k,l]*.
Comment calculer la distance entre plans successifs d'une même famille ?
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Rangées - suite
Construisez un réseau quelconque à trois dimensions, en appelant O l'origine.
Affecter les lettres A, B, C, D,E aux noeuds de coordonnées : 100, 010, 001, 111, 222.
Calculer les indices de la rangée OD puis ceux de la rangée OE.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Produit scalaire - définition
Il est nécessaire que nous revenions à la définition même du produit scalaire :
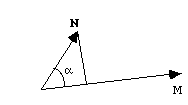
Soient deux vecteurs M et N; par définition leur produit scalaire est :
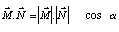
où
, 
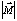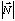
sont les normes des vecteurs M et N et α l'angle qui existe entre eux.
En particulier, on définit la norme de chacun des vecteurs par :
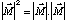
On peut encore dire que le produit scalaire du vecteur M par le vecteur N est égal au produit de la norme de M par la projection de N sur ce vecteur ... ou l'inverse, si vous préférez !
Cela vous suffit-il ?
- Oui ?
- Non ?
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Dernière chance!
Vous n'avez pas compris pourquoi les composantes d'un vecteur de l'espace cristallographique sont entières ?
Reprenons les choses au début, je vous laisse encore une chance ...
Il était une fois un vecteur V qui, à partir d'un point origine O, pointait sur un noeud. En exprimant son équation vectorielle sur la maille primitive on pouvait donc écrire :
V = ua + vb + w c.
a, b, c étaient donc trois translations non coplanaires parmi les plus courtes et l'extrémité de V ne pouvait donc être atteinte que par une combinaison entière de translations primitives.
En utilisant une maille multiple, V s'exprime, par contre, avec des composantes fractionnaires.
Le résultat du calcul d'un produit vectoriel, tel celui que nous venons d'étudier n'a, a priori, aucune chance d'exprimer des composantes entières ou rationnelles puisque les longueurs a, b, c sont des nombres décimaux. Donc le vecteur, résultat du calcul, n'exprime aucun vecteur physique de l'espace cristallographique.
En conclusion, cette géométrie est pleine de trous ! Les cristallographes ne s'intéressent pas à la définition d'une géométrie qui permettrait d'exprimer les coordonnées de n'importe quel point mais uniquement à ceux accessibles par des combinaisons de translations primitives, c'est à dire aux noeuds du réseau cristallin.
Si ceci reste incompréhensible, arrétons là ! Sinon, revenons au problème qui nous préoccupe : comment exprimer ln produit vectoriel?
Pour cela les cristallographes emploient un autre réseau appelé le réseau réciproque.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Le réseau réciproque hexagonal
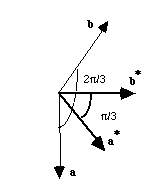
a* est perpendiculaire à b et contenu dans le plan a, b ou (001). Comme:
.
Si nous utilisons alors les relations scalaires qui permettent de définir le réseau réciproque :
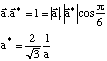
Par symétrie, puisque a = b, a* = b*i. La construction géométrique de a et b montre que:
.
c* est colinéaire à c car il est perpendiculaire à a et à b.
(Souvenez-vous que c* = 1/c).
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Erreur !
Ce n'est pas parce que ce cours est programmé qu'il ne faut pas réfléchir aux ordres de grandeur.
Regardez les formules. Toutes les quantités sont positives donc le cosinus recherché est positif et l'angle entre les plans ne peut être supérieur à 90degrés.
Incidemment, notez qu'un cosinus est toujours inférieur à l, ce qui permet un bon contrôle lorsqu'on calcule un angle car l'expression littérale doit aussi être plus petite que l'unité.
En cours de calcul si, manifestement, cela n'est plus vrai, c'est que vous avez fait une erreur.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Maille multiple
Vous vous êtes trompé.
Lorsquon définit une maille multiple, cela signifie que certains noeuds du réseau ne peuvent être atteints que par des fractions des translations du réseau : par exemple, dans une maille centrée, il existe une translation 1/2, 1/2, 1/2 qui permet d'atteindre le noeud situé au centre de la maille.
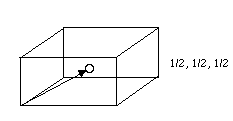
Dans ces conditions, un plan réticulaire peut couper les axes du repère, déterminé sur cette maille, en dehors des noeuds.
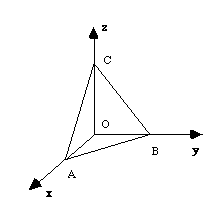
Par exemple, si nous considérons la maille évoquée précédemment, il existe un plan d'indices de Miller (111) qui contient le noeud 1/2, 1/2, 1/2 et qui coupe les axes en 3/2,0,0 ; 0,3/2,0 ; 0,0,3/2.
Il est facile de voir que les nombres x,y,z sont des nombres fractionnaires et que ce plan contient des noeuds dont les indices sont fractionnaires.
Cette notion de maille multiple ou maille primitive vous est-elle familière ?
- Oui ?
- Non ?
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996