@AFC_cristal
Produit vectoriel - plus d'explications
Le produit vectoriel de deux vecteurs A et B peut s'exprimer sous la forme d'un vecteur N tel que :
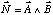
N est perpendiculaire à A et B donc au plan qu'ils définissent.
Sa longueur est définie par la surface du parallélogramme construit sur A et B:
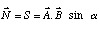
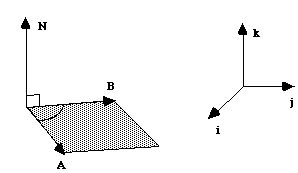
Dans un repère orthonormé ces règles deviennent très simples. Appellons i, j, k les trois vecteurs de la base:
.
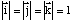La surface du parallélogramme déterminé par deux de ces vecteurs est égale à l'unité. On voit rapidement que :
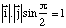
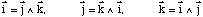
Surtout, souvenez-vous que le produit vectoriel n'est pas commutatif
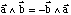
ni associatif
.
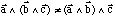Si cela n'est pas encore suffisant, arrétons là.
Sinon, continuez.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Etourdi(e)!
Vous répondez trop vite. Réécrivez les expressions de a*, b*, c* en utilisant les expressions scalaires.
Avant de cliquer, n'oubliez surtout pas que le produit d'un vecteur direct par un vecteur réciproque n'est plus 1.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Angles entre rangées
Après la théorie, voici la pratique.
Le réseau orthorhombique est un réseau cristallin où les vecteurs a, b, c de la base sont orthogonaux mais les longueurs sont différentes.
Voulez-vous calculer l'angle qui existe entre les rangées [123] et [321].
Lorsque vous aurez fini, continuez.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Rangée commune à deux plans réticulaires - suite
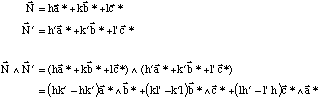
Si vous vous souvenez des remarques que nous avons faites sur les symétries des relations qui lient le réseau direct et le réseau réciproque, vous comprendrez que :
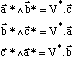
où V* est le volume de la maille réciproque.
Les indices de la rangée R sont proportionnels aux quantités qui apparaissent dans les parenthèses du produit vectoriel ; on retrouve très exactement les quantités u, v, w calculées précédemment.
D'un point de vue pratique, il suffit de se souvenir que les indices de la rangée commune aux plans d'indices de Miller (h,k,l) et (h',k',l') correspondent aux mineures associées à la troisième colonne du déterminant :
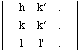
Exercice:
Calculez les indices de la rangée commune aux plans (123) et (132) puis continuez.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Indices de Miller - suite
OUI ! Les indices de Miller sont de la forme (0kl) car ce plan est parallèle à l'axe Ox.
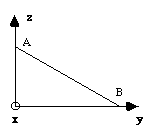
De façon générale, un plan est parallèle à un axe du repère lorsque l'indice correspondant est nul.
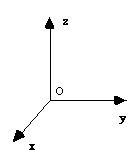
Ainsi le plan (100) est le plan Oy, Oz.
Le plan (010) correspond à Ox, Oz.
Le plan (001) correspond à Ox, Oy.
Envisageons une base orthogonale et le plan (120).
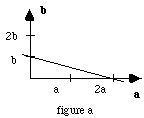
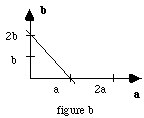
Sa trace, dans le plan Ox, Oy correspond à :
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Notions sur les plans réticulaires
Il me semble que vous avez compris la notion de rangée. Etudions maintenant la notion de plan réticulaire.
Un plan cristallographique (ou plan réticulaire) est un plan déterminé par les noeuds qu'il contient. On le définit par ses indices de Miller.
Imaginons un plan qui coupe les axes du repère quelconque en trois noeuds du réseau A, B, C.
Les unités choisies sur les trois axes sont a, b et c ; on peut écrire :
OA = x.a
OB = y.b
OC = z.c
Les coordonnées de A sont x,0,0 ; celles de B sont 0,y,0 et celles de C sont 0,0,z.
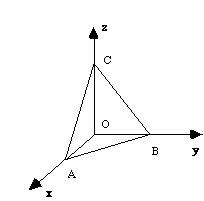
Si le repère x,y,z est construit sur une maille primitive (j'insiste bien primitive) x,y,z sont-ils entiers ?
- oui ?
- non ?
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Bien sûr !
Les vecteurs de composantes 2,4,2 et 1,2,1 sont tous deux colinéaires à la même droite.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Angle entre vecteurs
Le vecteur V colinéaire à la rangée [123] s'exprime par l'équation vectorielle :
.
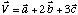De même le vecteur V' colinéaire à [321] s'écrit :
.
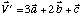Pour calculer l'angle qui existe entre ces deux vecteurs, nous allons calculer leur produit scalaire de deux manières différentes :
1) - Directement :
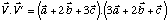
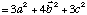
Si vous ne comprenez pas ce calcul, cliquez ici.
2) - Indirectement, à partir de la définition même du produit scalaire :
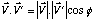
où φ est l'angle qui existe entre ces deux vecteurs.
Vous ne comprenez pas? Cliquez ici, sinon continuez :
= 
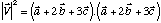
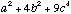
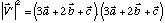
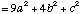
Donc l'angle qui existe entre les deux vecteurs est :
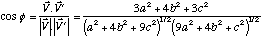
Si tout n'est pas parfaitement clair, retournez en arrière.
Sinon, nous continuons
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Calcul avec les produits vectoriels
L'équation vectorielle du vecteur [110] s'écrit :
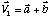
Celle du vecteur [111] est
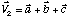
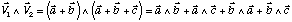
Rappelez-vous que le produit vectoriel d'un vecteur par un autre vecteur qui lui est colinéaire est nul.
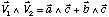
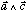est perpendiculaire à a et à c, donc colinéaire à b. Sa longueur est égale à la surface de dimension ac.
Donc
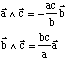
Les normes de a et b apparaissent au dénominateur car ni a ni b ne sont unitaires. Donc :
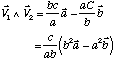
Si vous avez des difficultés, retournez en arrière, sinon, résolvez le problème suivant :
Calculez le produit vectoriel entre [110] et [111] lorsque la base vectorielle est absolument quelconque, c'est-à-dire ni normée ni orthogonale ;
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Exact
Encore faut-il le démontrer.
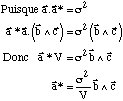
De même pour b* et c*. Comme le volume de la maille est le produit mixte des vecteurs de la base et que ceux-ci sont σ2 fois plus long qu'auparavant :
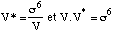
Le réseau réciproque vous semble peut-être une construction purement théorique. Je vais vous montrer qu'il est d'une grande utilité dans les calculs cristallographiques.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996