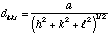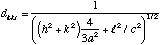@AFC_cristal
Rangées, normales....
Le dessin ci-dessous indique, dans les plans de base a,b (001) la trace du plan (1 -1 0) marquée T et la rangée [1 -1 0] marquée R.
La normale au plan est indiquée par N.
1) - On remarque que R et N, contenus dans les plans (001), ne sont pas colinéaires.
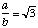
donc α = 60 degrés et β = 30 deg..
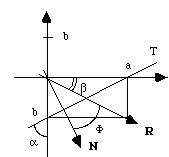
Si on examine attentivement les différents rectangles, on voit que l'angle entre R et N est:
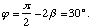
Donc, la normale à un plan n'est pas, en général, la rangée qui a pour indices les indices de Miller du plan.
Avez-vous trouvé la bonne solution ?
Si oui continuez; si vous avez seulement fait une faute de calcul, revoyez vos tables trigonométriques et continuez également!
Si vous avez mal orienté la rangée, retournez en arrière.
Vous êtes-vous trompé dans les indices du plan ? Revoyons ensemble les indices de Miller.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Début
Une rangée est une droite qui passe par des noeuds du réseau.
Bien sûr, il en existe une infinité puisque le réseau est infini mais cette infinité est plus petite que celle que vous connaissez en géométrie classique car nous avons uniquement défini les droites qui passent par les noeuds.
Une rangée est définie par ses indices notés entre crochets :
[u v w] où u, v, w sont des nombres entiers. Ces indices sont les composantes d'un vecteur équipollent à la rangée.
Cette définition identifie-t-elle une rangée de façon tout à fait précise ou laisse-t-elle planer une ambiguité ?
- Oui ? Elle définit bien une rangée.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Distance entre plans réticulaires
Soient deux plans immédiatement voisins P et P'. Q et Q' sont les projections de noeuds M et M' appartenant à chacun à un de ces plans sur la normale N commune à ces deux plans.
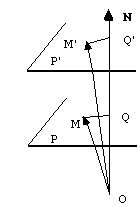
Alors :
OM.N = OQ.N = cte
OM'.N = OQ'.N = cte + 1
En calculant la différence entre ces deux équations, il vient:
(OQ' - OQ).N = 1.
OQ' - OQ est un vecteur dont la norme est la distance réticulaire entre les plans d'indices de Miller (h,k,l). On en déduit une formule bien connue qui exprime cete distance en fonction de la norme du vecteur N, normale à tous ces plans.
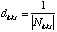
Il suffit donc de calculer la norme de la normale aux plans (h,k,l) pour pouvoir déterminer leur distance.
Comment la calculer ?
Tout simplement au moyen d'un produit scalaire exprimé dans le réseau réciproque.
Exercice:
Calculez la distance entre deux plans successifs d'une même famille dans un réseau hexagonal.
Eventuellement, recherchez l'expression des paramètres réciproques du réseau hexagonal.
Vous avez trouvé:
- 1 - 
- 2 - 
- 3 - Un autre résultat.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Rangées - ambiguitées
Un cristal contient des millions et des millions d'atomes, donc une quantité vertigineuse de droites (ou rangées) toutes parallèles entre elle. Cela n'aurait donc aucun sens physique de vouloir en discerner une ! Les propriétés physiques auxquelles la cristallographie et la physique du solide s'intéressent, sont liées aux orientations mais pas à la position d'un groupement particulier d'atomes ou d'une rangée précise dans le cristal.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Produit scalaire dans un réseau hexagonal
Un réseau hexagonal est défini de la façon suivante :
a = b, c
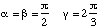
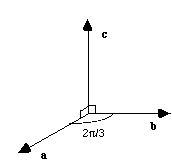
Si vous ne vous souvenez plus de ces notations, révisez les.
Calculez l'angle entre les rangées [135] et [111].
Cliquez ici lorsque vous aurez trouvé la solution.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Attention !
J'ai bien peur que vous n'ayez commencé à apprendre la cristallographie par le milieu !
Ce cours suppose que l'on ait déjà des notions élémentaires sur les réseaux et les symétries.
Il serait plus sage d'arréter ici et d'étudier d'abord les notions debase sur les réseaux cristallins. Si ce cours se révèle intéressant pour les étudiants, j'envisagerai de développer cette partie.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Le réseau réciproque hexagonal - suite
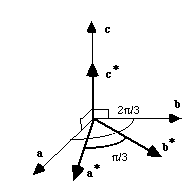
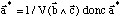est perpendiculaire au plan b, c.
Comme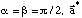 
est contenu dans le plan a, b. De même pour b*
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Angle entre deux plans (système hexagonal)
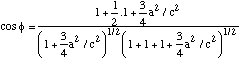
cos φ = 0.87
φ = 29 degrés 37'
Résolvez maintenant le problème suivant:
Considérons un réseau orthorhombique (a, b et c sont différents et les angles sont ous droits). Calculez l'angle entre les plans (011) et (0 -1 1), sachant que c/b = 1,5.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Maille multiple (à propos de ...)
Les nombres x, y, z peuvent effectivement être fractionnaires car une maille multiple contient des noeuds de coordonnées fractionnaires.
Si la raison pour laquelle vous êtes venu ici est autre, approfondissez cette question en cliquant ici.
Est-ce que le plan déterminé par les indices de Miller (hkl) est unique ?
- Oui ?
- Non ?
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
Erreur!
NON ! Les deux plans ont mêmes indices de Miller car (111) et (222) sont proportionnels et nous avons vu que nous déterminions une famille de plans parallèles sans nous préoccuper d'un plan, en particulier.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996