Rangées - indices d'une rangée
Les indices de la rangée BF sont ceux d'un vecteur colinéaire, BF, par exemple.
Or, BF = OF - OB, donc les composantes recherchées sont: -1 -1 -1, ce qui est équivalent à la rangée [111] déjà étudiée.
Comme nous nous intéressons aux familles de rangées, c'est-à-dire à des droites parallèles entre elles, le vecteur colinéaire qui détermine la rangée ne nous intéresse qu'au point de vue de son orientation ; sa longueur n'a aucune importance ni son origine et nous choisirons toujours les indices d'une rangée de façon qu'ils soient premiers entre eux.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Produit vectoriel (généralisation)
La notion de produit vectoriel est moins évidente lorsque on utilise des bases vectorielles non normées.
Par exemple, envisageons une base orthorhombique:
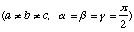
Voulez-vous calculer le produit vectoriel entre les vecteurs [110] et [111] ?
Cliquez ici après avoir fait le calcul.
Ne trichez pas!

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Et encore et toujours le réseau réciproque
Celui de la maille réciproque est : 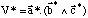

Exprimons ces trois vecteurs en utilisant les produits vectoriels qui les lient aux vecteurs du réseau direct:
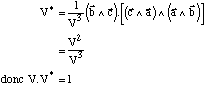
Les volumes des mailles directe et réciproque sont inverses l'un de l'autre.
Certains physiciens définissent le réseau réciproque avec des relations légèrement différentes :
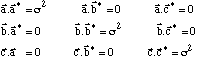
On introduit donc une constante différente de l'unité ; par exemple, en Physique du Solide:
σ2 = 2π .
En utilisant cette nouvelle définition, réécrivez les expressions vectorielles de a*, b*, c* en fonction de a, b, c puis la relation entre V et V*.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Rappel sur les réseaux
Vous devriez peut-être revoir votre cours de cristallographie à l'endroit où l'on définit les réseaux (cette notion n'est pas encore incluse dans ce cours).
Si le plan réticulaire coupe l'axe x au point A, et si le réseau est construit sur trois translations parmi les plus courtes, non coplanaires, alors le point A qui est contenu dans le plan réticulaire mais aussi dans la rangée OA, est forcément un noeud du réseau. Comme le réseau est primitif OA est un nombre entier de fois la translation unitaire a.
OA = x.a donc x est entier.
Le raisonnement est le même pour y et z.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Rangée commune à deux plans réticulaires
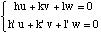
Utilisons w comme inconnue auxiliaire et calculons u et v :
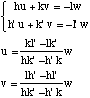
Posons : 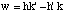
Les indices de la rangée commune aux deux plans sont donc:
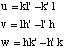
2) Nous allons expliquer maintenant une deuxième méthode pour déterminer les indices de la rangée R.
La rangée recherchée R est perpendiculaire aux normales N et N' aux deux plans. Elle est donc parallèle au produit vectoriel de ces deux vecteurs. Il suffit donc d'exprimer ce produit vectoriel pour trouver les indices de la rangée recherchée.
Remarquons une très jolie astuce:
N et N' sont des vecteurs de l'espace réciproque. Leur produit vectoriel est un vecteur de l'espace direct en vertu des relations vectorielles qui expriment les vecteurs directs en fonction des vecteurs réciproques. Ceci est cohérent puisque la rangée R est l'intersection de deux plans directs.
Calculez ce produit vectoriel .

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Indices de Miller - suite
Vous n'avez pas encore vraiment saisi la notion d'indices de Miller : ils sont inversement proportionnels aux distances auxquelles un plan de cete famille coupe les axes cristallographiques. Donc, si ce plan est parallèle à un axe, comme il le coupe à l'infini, l'inverse de cette distance est nul et l'indice de Miller correspondant est 0.
Vous sentez-vous maintenant éclairé ?
Oui ?
Non ?

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Plans réticulaires...
Mais non ! Il existe la même ambiguïté que pour les rangées : imaginez un plan parallèle à ABC qui coupe aussi les axes cristallographiques, mais en des noeuds de coordonnées x', y', z'.
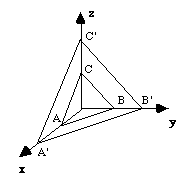
Alors : x/x' = y/y' = z/z'. Si on calcule les inverses de x', y', z' : 1/x', 1/y', 1/z'.
Ils seront donc proportionnels entre eux et, si on les multiplie par leur plus petit commun multiple, on obtiendra les même nombres h,k,l.
Les indices de Miller de ce plan sont donc les mêmes que ceux de ABC et (hkl) caractérise une famille de plans parallèles entre eux.
Etes-vous vraiment chagriné de ne pas pouvoir déterminer un plan de façon unique ? Allez donc vous consoler!
Continuez si vous êtes un esprit heureux et sans problème.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Notions sur les rangées réticulaires
Une rangée est une droite qui passe par des noeuds du réseau.
Bien sûr, il en existe une infinité puisque le réseau est infini mais cette infinité est plus petite que celle que vous connaissez en géométrie classique car nous avons uniquement défini les droites qui passent par les noeuds.
Une rangée est définie par ses indices notés entre crochets :
[u v w] où u, v, w sont des nombres entiers. Ces indices sont les composantes d'un vecteur équipollent à la rangée.
Cette définition identifie-t-elle une rangée de façon tout à fait précise ou laisse-t-elle planer une ambiguité ?
- Oui ? Elle définit bien une rangée.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Oui !
Il existe une infinité de droites parallèles à un même vecteur. On ne définit donc pas une droite par les indices d'une rangée mais un ensemble de droites toutes parallèles entre elles.
Si cette explication vous satisfait, continuez.
S'il vous semble nécessaire de pouvoir définir une droite de façon unique, dans un espace cristallographique, cliquez ici.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Produit scalaire - suite
Les équations vectorielles des deux vecteurs sont :
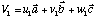
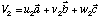
et le produit scalaire s'exprime donc :
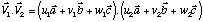
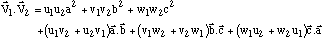
On peut remplacer les produits scalaires entre les vecteurs de la base par leur expression si on suppose connus les angles qui existent entre ces vecteurs.
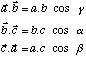
Les angles sont repérés de façon standard par la lettre grecque qui correspond au vecteur auquel l'angle est opposé.
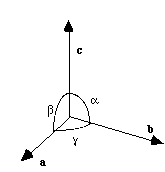
Vous aviez trouvé ce résultat et tout est clair ?
- Oui
- Vous vous êtes trompés et il vous faut une explication complémentaire? Continuez.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996






