Produit scalaire

Nous allons maintenant envisager la notion de produit scalaire, dans l'espace cristallographique.

Très rapidement vous vous apercevrez si vos notions sont suffisantes, mais ne négligez pas cette question ; nombreux sont ceux qui se laissent prendre par ces notions simples.

Soit un réseau quelconque défini sur une base vectorielle sans aucune caractéristique particulière : nous appellerons a, b, c les vecteurs de cette base. Soient deux vecteurs:
.

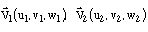Calculez leur produit scalaire.

Après avoir fait le calcul, cliquez ici.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Angle entre plans réticulaires

En cristallographie on définit l'angle entre deux plans par l'angle de leurs normales, c'est-à-dire que l'on calcule l'angle entre deux rangées du réseau réciproque.

Soient deux plans d'indices de Miller (h,k,l) et h',k'l').

Les équations de leurs normales respectives sont :

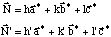
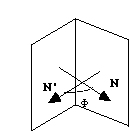
On calcule alors l'angle de ces rangées comme vous avez déjà appris à le faire. La seule différence est que maintenant ce calcul s'efféctue dans le réseau réciproque.

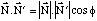
Donc,

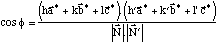
Pour terminer le calcul, il faut exprimer les produits scalaires entre vecteurs de la base réciproque, c'est à dire connaitre leurs normes et les angles qu'ils déterminent. Vous avez déjà appris à le faire.

Application :

Etablissez la formule qui donne l'angle entre deux plans dans un réseau hexgonal.

Si vous ne savez plus calculer les normes ni les angles entre vecteurs de la base réciproque hexagonale, rafraichissez vous la mémoire.

Lorsque vous aurez effectué ce calcul et résolu ce problème, continuez.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Rangées - suite

Le vecteur OD, colinéaire à la rangée OD a pour composantes [111], le vecteur OF a pour composantes [222] mais ils sont supportés par une même droite. Il s'agit donc de la même rangée.

Continuez

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Angle entre vecteurs dans un réseau hexagonal

On définit un vecteur colinéaire à chacune de ces deux rangées :

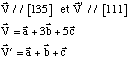
Comme dans l'exercice précédent, nous allons exprimer le produit scalaire de ces deux vecteurs de deux façons différentes:

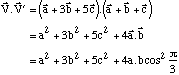
Comme a = b :

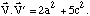
J'espère que vous vous souvenez de la valeur de
.

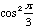Sinon, au revoir!

Exprimons maintenant le produit scalaire avec les normes des vecteurs :

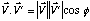
où φ est l'angle entre V et V'.

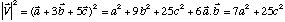
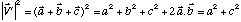
Donc,

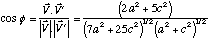
Est-ce vraiment compris ?

- Oui ?

- Non ?

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Réseau réciproque - résultat du calcul 

Le résultat est:

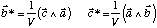
Expliquons ce calcul.

b* est perpendiculaire à a puisque a.b* = 0.

De la même façon b* est perpendiculaire à c car b*.c = 0. Comme b* est perpendiculaire à la fois à ces deux vecteurs, il est parallèle à leur produit vectoriel et on peut écrire :

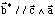
Comme b.b* = 1, on en déduit que:

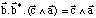
Or,

où V est le volume de la maille.

Soit finalement

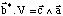
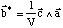
La démonstration est identique pour c*.

Si vous n'avez pas été capable de trouver vous-même ce résultat, exercez-vous en faisant le calcul complet pour c*.

Les produits scalaires qui définissent le réseau réciproque sont symétriques :
cela signifie que, connaissant a*, b*, c* le même raisonnement permet d'exprimer les vecteurs de base du réseau direct:

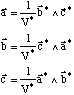
Calculez maintenant la relation entre le volume de la maille réciproque et celui de la maille directe. Pour cela écrivez les deux produits mixtes et regardez leurs relations.

Qu'en concluez-vous quant aux dimensions du réseau réciproque ?

• V = V*. Le réseau réciproque est une deuxième base de l'espace cristallographique .
• V = 1/V*, les dimensions du réseau réciproque sont les inverses de longueurs.
• V* est une expression compliquée de a,b,c et dépend des angles entre ces vecteurs ; les dimensions du réseau réciproque sont inverses de celle du réseau direct .
• Vous avez trouvé la solution et vous avez l'intime conviction qu'elle est juste ; le réseau réciproque est d'un grand intérêt et vous avez tout compris.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Ne désespérez pas!

Certes, V* dépend de a, b, c puisqu'on exprime les vecteurs réciproques à l'aide des vecteurs directs.

L'expression de V peut être compliquée car le produit mixte (a, b, c) n'est pas toujours simple à calculer.

Réfléchissez sur la symétrie des relations qui lient vecteurs directs et réciproques puis choisissez une autre réponse.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Angles entre plans réticulaires (système orthorhombique)

Surtout, ne déterminez pas les vecteurs du réseau réciproque !

Il existe une solution géométrique beaucoup plus simple: dessinez la trace des plans (011) et (0-11) dans le plan (100) :

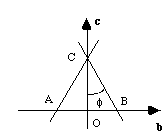
OA = -b, OB = b, OC = c

La trace de (011) est BC, celle de (0-11) est AC.

Vous pouvez éventuellement revoir la définition des indices de Miller.

Comme c/b = 1,5, tg φ = b/c = 1/1,5
donc

φ = 33,69 degrés

Vous pourriez retrouver ce résultat à l'aide du réseau réciproque mais reconnaissez qu'il ne sert à rien d'utiliserer un canon pour tuer une mouche !

Continuez.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Plans réticulaires

Imaginez un réseau quelconque ; portez les noeuds A,B,C,D,E et F de coordonnées : 100, 010, 001, 200, 020, 002.

Quels sont les indices de Miller du plan ABC puis ceux du plan DEF ?

- (111) tous les deux.

- (111) pour ABC, (222) pour DEF.

- (111) pour ABC, (1/2, 1/2, 1/2) pour DEF.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Indices de Miller (toujours...)

Vous vous êtes souvenus que les indices de Miller sont inversement proportionnels aux distances auxquels ce plan coupe les axes, mais vous avez oublié qu'on multiplie les nombres obtenus par leur plus petit commun multiple de façon à obtenir un triplet de nombres entiers premiers entre eux.
La bonne réponse est donc :

- (111) ?

- (222) ?

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996

Produit vectoriel

Le produit vectoriel peut être représenté, dans un espace à trois dimensions, par un vecteur.

Si la base est orthonormée, appelons I, J, K les vecteurs unitaires de cette base.

Alors :

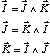
Cela vous suffit-il ?

Si oui continuons, sinon rafraîchissez vos connaissances.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996