@AFC_cristal
Produit vectoriel - résultat du calcul
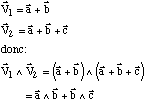
Si la base est quelconque, il n'est pas évident d'exprimer le vecteur résultant sur la base a, b, c. et le produit vectoriel devient donc très difficile à calculer.
De plus, en cristallographie, nous ne nous intéressons qu'aux vecteurs qui pointent sur les noeuds du réseau, c'est à dire à ceux dont les composantes sont entières lorsqu'on les exprime dans une maille primitive.
A priori, le résultat du calcul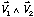 
n'a aucune chance de donner un vecteur de coordonnées entières donc le résultat n'exprime pas un vecteur de l'espace cristallographique.
Si nous revenons au résultat trouvé pour ce même exercice lorsque la base est orthogonale, nous avions trouvé :
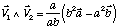
Ce vecteur, bien que nous connaissions son expression sur la base a, b, c, n'appartient pas non plus à l'espace cristallographique, car ses composantes ne sont pas entières. Le produit vectoriel ne semble donc offrir aucun intérêt pour le cristallographe car il ne sait pas l'exprimer dans la plupart des cas.
Mais, comme nous ne manquont pas de ressources, nous avons trouvé une solution!
Accrochez-vous à votre souris: nous allons introduire le réseau réciproque.
Si vous n'avez pas compris pourquoi j'insiste sur l'idée que les composantes d'un vecteur exprimées sur une base primitive, sont entières, revenons en arrière.
Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996
