Calculs cristallographiques - Indices de Miller

Plans réticulaires...

Mais non ! Il existe la même ambiguïté que pour les rangées : imaginez un plan parallèle à ABC qui coupe aussi les axes cristallographiques, mais en des noeuds de coordonnées x', y', z'.

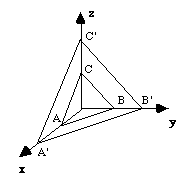
Alors : x/x' = y/y' = z/z'. Si on calcule les inverses de x', y', z' : 1/x', 1/y', 1/z'.

Ils seront donc proportionnels entre eux et, si on les multiplie par leur plus petit commun multiple, on obtiendra les même nombres h,k,l.

Les indices de Miller de ce plan sont donc les mêmes que ceux de ABC et (hkl) caractérise une famille de plans parallèles entre eux.

Etes-vous vraiment chagriné de ne pas pouvoir déterminer un plan de façon unique ? Allez donc vous consoler!

Continuez si vous êtes un esprit heureux et sans problème.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996