Calculs cristallographiques - réseau réciproque

Réseau réciproque - résultat du calcul 

Le résultat est:

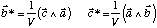
Expliquons ce calcul.

b* est perpendiculaire à a puisque a.b* = 0.

De la même façon b* est perpendiculaire à c car b*.c = 0. Comme b* est perpendiculaire à la fois à ces deux vecteurs, il est parallèle à leur produit vectoriel et on peut écrire :

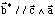
Comme b.b* = 1, on en déduit que:

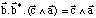
Or,

où V est le volume de la maille.

Soit finalement

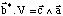
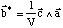
La démonstration est identique pour c*.

Si vous n'avez pas été capable de trouver vous-même ce résultat, exercez-vous en faisant le calcul complet pour c*.

Les produits scalaires qui définissent le réseau réciproque sont symétriques :
cela signifie que, connaissant a*, b*, c* le même raisonnement permet d'exprimer les vecteurs de base du réseau direct:

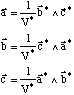
Calculez maintenant la relation entre le volume de la maille réciproque et celui de la maille directe. Pour cela écrivez les deux produits mixtes et regardez leurs relations.

Qu'en concluez-vous quant aux dimensions du réseau réciproque ?

• V = V*. Le réseau réciproque est une deuxième base de l'espace cristallographique .
• V = 1/V*, les dimensions du réseau réciproque sont les inverses de longueurs.
• V* est une expression compliquée de a,b,c et dépend des angles entre ces vecteurs ; les dimensions du réseau réciproque sont inverses de celle du réseau direct .
• Vous avez trouvé la solution et vous avez l'intime conviction qu'elle est juste ; le réseau réciproque est d'un grand intérêt et vous avez tout compris.

Retour au plan du cours.
Copyright Yves Epelboin, Université P.M. Curie, Paris, France, 1979-1996