Symétrie

EXACT

Un trapèze est une figure non symétrique. Toutefois, il est possible d'arranger des trapèzes de façon à former des figures symétriques.

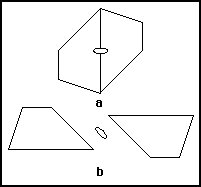
En juxtaposant deux trapèzes identiques comme sur la figure a, il apparaît un point de rotation binaire au milieu du côté commun.

Nous pouvons également placer les trapèzes de telle façon que chaque côté de l'un soit parallèle au côté correspondant de l'autre. Il apparaît encore un point de rotation binaire.

En principe, il n'y a là rien de nouveau car nous pouvons considérer le plan entier avec deux trapèzes formant une figure unique. Il faut alors chercher les éléments de symétrie de cette figure, à savoir le point de rotation binaire. ( voir figures a et b )

Si nous faisons de même avec, par exemple, le rectangle ( la figure est alors constituée de deux rectangles identiques ), nous obtenons les mêmes éléments de symétrie que pour un seul rectangle.

Question :

Peut-on avoir une ligne-miroir dans un plan avec deux trapèzes identiques?

Réponses :

a) Non

b) Oui

Retour au plan du cours.
Page modifiée le: 28/03/03  
© H.SCHENK Laboratoire de Cristallographie, Université d'Amsterdam, Pays-Bas, et  LMCP, France.