Symétrie

EXACT

Au milieu des côtés de la maille élémentaire telle qu'elle a été choisie dans le problème précédent, se trouvent des points de rotation binaire. Le moulin A vient en coïncidence avec le moulin B par la rotation binaire autour du point etc. ...

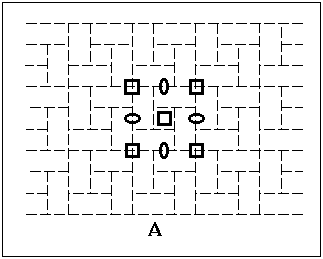
La maille élémentaire ne contient pas d'autre élément de symétrie de telle sorte que la symétrie complète de la maille élémentaire corresponde à la figure B. Un tel arrangement périodique d'éléments de symétrie est appelé groupe plan. Le nom de ce groupe plan est p4.

Cliquez ici pour faire apparaître le dessin de tous les groupes plans qui existent. Il s'affichera dans une nouvelle fenêtre que nous vous conseillons de laisser visible à l'écran.

A l'aide des mêmes moulins, on peut construire un autre dessin périodique, tel que chaque "aile" appartienne à deux moulins différents.

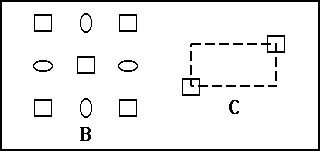
Nous pouvons choisir, par exemple, deux sommets opposés comme points de rotation quaternaire (figure C).

Souvenez-vous que sous l'action des points de rotation, les autres points de rotation quaternaire se répètent eux-mêmes.

Questions:

Y a-t-il :

a) Seulement des moulins - D ?

b) Seulement des moulins - G ?

c) A la fois des moulins - D et des moulins - G ?

Retour au plan du cours.
Page modifiée le: 28/03/03  
© H.SCHENK Laboratoire de Cristallographie, Université d'Amsterdam, Pays-Bas, et  LMCP, France.